My first program. Roman Numerals.

In our previous post we learned about Excel functions and how to write our own functions in Excel’s built-in code editor. We also learned about testing and refactoring. Today we put all that into action and write our first program.

To learn to program you have to practice. So, do have Excel open as you read this article. We are going to be entering code then editing it, so it only really works if you are following along in Excel yourself. And don’t forget to save as you go, Excel does have a habbit of freezing from time to time, especially when we get to loops. It can be frustrating to have to start from scratch and it is a good habbit to get into.

Putting it all together: Roman Numerals

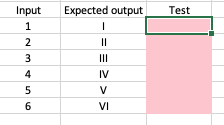
We are going to write a function that converts a number into its Roman Numeral equivalent. We start with some tests: numbers in one column and strings I, II, III, and so on, in the cells next to them. The test column will contain calls to our conversion function taking the input column as its argument. See our previous article if you can’t remember how to set-up conditional formatting. The tests initially show red for fail because we haven’t written the conversion function yet. We are going to gradually make the tests pass.

Roman Numerals first tests

Roman Numerals: start with failing tests

The next step is to get a trivially simple function in place to check that we remembered how to open the VBA editor, add a module, get the syntax for a function right and call that function from the sheet. None of that has anything to do with Roman Numerals, but we don’t want to be messing around with any of that when we come to thinking about the actual problem. This is very common in programming and is known as “Hello, world!”. It simply means doing the simplest thing possible that proves the underlying technology is working, regardless of what that technology is being used for. We create a function called n2r (number to roman) which takes a number and returns a string containing the numeral, such as XVI. To start with we will return Hello, world!. Remember in VBA we set the return value of a function by setting the function name equal to the value we want to return:

Public Function n2r(n As Integer) As String
  n2r = "Hello, world!"
End Function

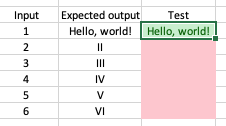
I have also modified the test, as the expected output from this function is Hello, world!. This checks that our conditional formatting works and is not just stuck on red, testing the tests if you like.

First passing test

Hello, world!

OK, we are all set-up. All that remains is to write some code and make our tests pass. The general approach is to extend n2r so that more and more tests pass. In the short-term we can just use our friend the IF function, or its VBA equivalent, like this:

Public Function n2r(n As Integer) As String
  If n = 1 Then
    n2r = "I"
  ElseIf n = 2 Then
    n2r = "II"
  ElseIf n = 3 Then
    n2r = "III"
  ElseIf n = 4 Then
    n2r = "IV"
  ElseIf n = 5 Then
    n2r = "V"
  ElseIf n = 6 Then
    n2r = "VI"
  ElseIf n =7 Then
    n2r = "VII"
  ElseIf n = 8 Then
    n2r = "VIII"
  End If
End Function

Three tests

More tests passing

This approach is fine for small numbers but is not really solving the problem in general. For numerals such as I, II and III we know each figure stands for each unit in the number, so we could build up the numeral with a loop, in this case a While loop, which keeps looping while the condition is true. When it isn’t it continues with the rest of the program.

Note: Be careful to ensure the condition changes on each iteration of the loop, i.e. change the value of n, otherwise it will never exit the loop and Excel hangs.

So, let’s replace the first three clauses in the IF statement with a loop, and check that the tests still pass:

Public Function n2r(n As Integer) As String
  While n > 0 And n <= 3
    n2r = n2r + "I"
    n = n - 1
  Wend

  If n = 4 Then
    n2r = "IV"
  ElseIf n = 5 Then
    n2r = "V"
  ElseIf n = 6 Then
    n2r = "VI"
  ElseIf n = 7 Then
    n2r = "VII"
  ElseIf n = 8 Then
    n2r = "VIII"
    End If
End Function

The important thing here is that the we have improved the code and the tests still pass, i.e. we have green cells in our sheet. Improving the code design while not changing the status of the tests is called refactoring. Does this change suggest any further improvements? Well, the I, II, III appears in the numerals for 6, 7 and 8, so if we subtract 5, add a V to our resulting string then put it through the same code for 1, 2 and 3 we should get the same result. We will need to move the 1,2,3 code to the end to do that.

Public Function n2r(n As Integer) As String
  If n = 4 Then
    n2r = "IV"
  ElseIf n >= 5 Then
    n2r = "V"
    n = n - 5
  End If
  
  While n > 0 And n <= 3  ' MOVED DOWN
    n2r = n2r + "I"
    n = n - 1
  Wend
End Function

The tests up to eight still pass. Let’s push on to ten. As before we start with the naive approach, using IF.

Public Function n2r(n As Integer) As String
  If n = 4 Then
    n2r = "IV"
  ElseIf n = 9 Then   ' <= NEW
    n2r = "IX"        ' <= CODE
  ElseIf n = 10 Then  ' <= HERE
    n2r = "X"         ' <= & HERE
  ElseIf n >= 5 Then
    n2r = "V"
    n = n - 5
  End If
  
  While n > 0 And n <= 3
    n2r = n2r + "I"
    n = n - 1
  Wend
End Function

The test pass. Let’s keep going and add 11, and see if any further patterns emerge:

Public Function n2r(n As Integer) As String
  If n = 4 Then
    n2r = "IV"
  ElseIf n = 9 Then
    n2r = "IX"
  ElseIf n = 10 Then
    n2r = "X"
  ElseIf n = 11 Then  ' <= MORE CODE
    n2r = "XI"        ' <= HERE
  ElseIf n >= 5 Then
    n2r = "V"
    n = n - 5
  End If
  
  While n > 0 And n <= 3
    n2r = n2r + "I"
    n = n - 1
  Wend
End Function

Yes, the numbers above ten are like the numbers above five. They are just X with a string of Is after it. So let’s do to ten and above what we did to five and above, put in an X and subtract 10.

Public Function n2r(n As Integer) As String
  If n = 4 Then
    n2r = "IV"
  ElseIf n = 9 Then
    n2r = "IX"
  ElseIf n >= 10 Then  ' <= CHANGE FOR
    n2r = "X"          ' <= CODE FOR 10
    n = n - 10         ' <= DELETE CODE FOR 11
  ElseIf n >= 5 Then
    n2r = "V"
    n = n - 5
  End If
  
  While n > 0 And n <= 3
    n2r = n2r + "I"
    n = n - 1
  Wend
End Function

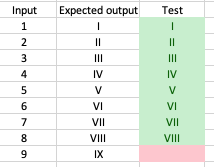
Great, that get’s us up to 13. Fourteen fails but we continue the pattern of adding a naive implementation with the expectation of refactoring later.

Public Function n2r(n As Integer) As String
  If n = 4 Then
    n2r = "IV"
  ElseIf n = 9 Then
    n2r = "IX"
  ElseIf n = 14 Then  ' <= NEW
    n2r = "XIV"       ' <= CODE
  ElseIf n >= 10 Then
    n2r = "X"
    n = n - 10
  ElseIf n >= 5 Then
    n2r = "V"
    n = n - 5
  End If
  
  While n > 0 And n <= 3
    n2r = n2r + "I"
    n = n - 1
  Wend
End Function

The case for fourteen, XIV reminds us that it is just X plus IV. But we already have code for adding X and IV to our string. Spotting repetition like this is often a clue to a deeper structure and hence improved code structure. The general rule is “Don’t Repeat Yourself”, and fixing it is referred to as DRYing-up code. We aren’t quite ready for that yet though.

Let’s add IV on to whatever we have left after subtracting X, by moving it further down the script, and remove the special case for fourteen.

Public Function n2r(n As Integer) As String
  If n = 9 Then        ' <= CHANGE ELSEIF TO IF
    n2r = "IX"
  ElseIf n >= 10 Then
    n2r = "X"
    n = n - 10
  ElseIf n >= 5 Then
    n2r = "V"
    n = n - 5
  End If

  If n = 4 Then        ' <= MOVED FROM ABOVE
    n2r = n2r + "IV"   ' <= APPEND TO WHAT'S
  End If               ' <= LEFT

  While n > 0 And n <= 3
    n2r = n2r + "I"
    n = n - 1
  Wend
End Function

And the tests up to fourteen still pass. The test for fifteen is failing and we can see that it is returning X without appending a V. That is easy to fix by changing the ELSEIF to an IF so it gets run as well as the code for X rather than instead of it.

Public Function n2r(n As Integer) As String
  If n = 9 Then
    n2r = "IX"
  ElseIf n >= 10 Then
    n2r = "X"
    n = n - 10
  End If               ' <= TIDY UP THE IF 
        
  If n >= 5 Then       ' <= CHANGE ELSEIF TO IF
    n2r = n2r + "V"    ' <= AND APPEND 
    n = n - 5
  End If

  If n = 4 Then
    n2r = n2r + "IV"
  End If

  While n > 0 And n <= 3
    n2r = n2r + "I"
    n = n - 1
  Wend
End Function

Oh dear, that didn’t work and we have broken nine too. This shows the value of tests as regression checkers.

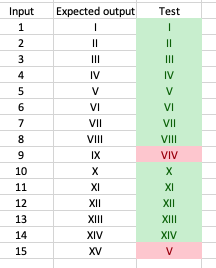
Unexpected test failure

A bug! Unexpected failure of the test for 9

After staring at our code for a bit we realise that the code for IX does not reduce n by nine, so the case for five, which is n being bigger than five, is also triggered. That is easy to fix.

Public Function n2r(n As Integer) As String
  If n = 9 Then
    n2r = "IX"
    n = n - 9          ' <= BUG FIX
  ElseIf n >= 10 Then
    n2r = "X"
    n = n - 10
  End If
        
  If n >= 5 Then
    n2r = n2r + "V"
    n = n - 5
  End If

  If n = 4 Then
    n2r = n2r + "IV"
  End If

  While n > 0 And n <= 3
    n2r = n2r + "I"
    n = n - 1
  Wend
End Function

The tests all pass. We can tidy things up a bit. We can reorder the if clauses into numerical order, biggest first. Also the n = 9 and n = 4 tests could just as well be n >= 9 and n >= 4 and would make them like all the other tests. And they could append to n2r rather than just setting it. As ever we check that this does not break any tests.

Public Function n2r(n As Integer) As String
  If n >= 10 Then
    n2r = n2r + "X"  '<= APPEND 
    n = n - 10
  End If

  If n >= 9 Then
    n2r = n2r + "IX" '<= APPEND
    n = n - 9
  End If
        
  If n >= 5 Then
    n2r = n2r + "V"
    n = n - 5
  End If

  If n >= 4 Then     '<= MAKE >=
    n2r = n2r + "IV"
  End If

  While n > 0 And n <= 3
    n2r = n2r + "I"
    n = n - 1
  Wend
End Function

The two odd ones out are the If n>=4 clause and the While loop. We can make the If n >= 4 clause the same as the others by adding a n = n - 4 statement. That would also mean that by the time we reach the while loop we know n must be less than four, so we can simplify that test too.

Public Function n2r(n As Integer) As String
  If n >= 10 Then
    n2r = n2r + "X"
    n = n - 10
  End If

  If n >= 9 Then
    n2r = n2r + "IX"
    n = n - 9
  End If
        
  If n >= 5 Then
    n2r = n2r + "V"
    n = n - 5
  End If

  If n >= 4 Then
    n2r = n2r + "IV"
    n = n - 4        ' <= ADD THIS
  End If

  While n >= 1       ' <= SIMPLIFY THIS
    n2r = n2r + "I"
    n = n - 1
  Wend
End Function

OK great. How far will this take us? We add tests up to twenty. They all pass except twenty and we can fix that, as before, but using While rather than an If:

    Public Function n2r(n As Integer) As String
      While n >= 10
        n2r = n2r + "X"
        n = n - 10
      Wend
      ' REMAINING CODE HERE

That fixes twenty and we can add more tests, all the way to forty which is the next special case, XL because fifty is L. After adding the tests, let’s add the code to make them pass.

    Public Function n2r(n As Integer) As String
      If n >= 50
        n2r = n2r + "L"
        n = n - 50
      End If

      If n >= 40
        n2r = n2r + "XL"
        n = n - 40
      End If
      ' REMAINING CODE HERE

Great, we have tests passing up to fifty and beyond. But the code is looking very repetative. It needs DRYing up.

It is a mix of Whiles and Ifs, but if we used a while statement instead of an if it would be all while statements. Then we could extract the while block into a function of its own and just call it everywhere there is a while block.

In fact a while does contain an implicit if, because it checks the clause and if it is true it executes the loop code, else it does not. So we can use a while instead of an if:

Public Function n2r(n As Integer) As String
  While n >= 50
    n2r = n2r + "L"
    n = n - 50
  Wend

  While n >= 40
    n2r = n2r + "XL"
    n = n - 40
  Wend

  While n >= 10
    n2r = n2r + "X"
    n = n - 10
  Wend

  While n >= 9
    n2r = n2r + "IX"
    n = n - 9
  Wend

  While n >= 5
    n2r = n2r + "V"
    n = n - 5
  Wend

  While n >= 4
    n2r = n2r + "IV"
    n = n - 4
  Wend

  While n >= 1
    n2r = n2r + "I"
    n = n - 1
  Wend
End Function

This now looks ripe for a refactoring.

We create a function that takes the running total, the string representing the roman numeral to be appended and the value to be knocked off the running total. The string is returned (remember in VBA this is done by setting the function name equal to whatever you want returned) so that it can be passed on.

Public Function f(ByRef i As Integer, ByVal numeral As String, ByVal value as Integer) As String
   While i >= value
      f = f + numeral
      i = i - value
   Wend
End Function

All that remains now is to replace the while blocks with calls to this function. We try one to check it works (all the tests pass) by commenting out the code we will delete, before actually deleteing all the code. Alternatively if you are confident using the undo function, you can just delete the code:

Public Function n2r(n As Integer) As String
'  While n >= 50
'    n2r = n2r + "L"
'    n = n - 50
'  Wend
  n2r = n2r + f(n, "L", 50)
  ' REMAINING CODE HERE

That works, so we can can replace all the while blocks.

Public Function n2r(n As Integer) As String
  n2r = n2r + f(n,  "L", 50)
  n2r = n2r + f(n, "XL", 40)
  n2r = n2r + f(n,  "X", 10)
  n2r = n2r + f(n, "IX", 9)
  n2r = n2r + f(n,  "V", 5)
  n2r = n2r + f(n, "IV", 4)
  n2r = n2r + f(n,  "I", 1)
End Function

Much better! And we can go further using VBA’s continuation lines. Now that the structure of the code is very clear we can add all the remaining special cases for 90, 100, 400 etc. The final code looks like this:

Public Function n2r(n As Integer) As String
  n2r = f(n,  "M", 1000) + _
        f(n, "CM",  900) + _
        f(n,  "D",  500) + _
        f(n, "CD",  400) + _
        f(n,  "C",  100) + _
        f(n, "XC",   90) + _
        f(n,  "L",   50) + _
        f(n, "XL",   40) + _
        f(n,  "X",   10) + _
        f(n, "IX",    9) + _
        f(n,  "V",    5) + _
        f(n, "IV",    4) + _
        f(n,  "I",    1)
End Function

Public Function f(ByRef i As Integer, ByVal numeral As String, ByVal value as Integer) As String
   While i >= value
      f = f + numeral
      i = i - value
   Wend
End Function

And of course we should test it:

Test big numbers

Test on large numbers

What we have ended up with is a very elegant solution that is tested to a high degree of certainty. The process to achieve this can be repeated for all programming tasks:

Write a test
Write some naive code to make the test pass
Check that all the tests still pass
Refactor
Repeat

This is sometimes referred to as the “red green refactor” loop, as the failing test usually displayed in red and making it pass turns it green. Notice how it is enabled by building a test suite as you progress. Without the tests, continually altering the code would be a risky business. But with them, you quickly know if your change has broken anything and therefore where to concentrate your efforts on getting back to a working set of tests. This avoids getting stuck for long periods wondering where a bug might be. It is always in the last thing you did, so just undo it and try again. Not getting stuck for long periods means you can be highly productive. And you get elegant, well-designed, well-tested code too.

In a future article we will move from Excel and VBA into Python. We use the same techniques of testing and refactoring, just in a different technical environment. See you next time.